Background

CrackMe Name: Mars Analytica
CrackMe Author: Towel

CrackMe Description:
Give it the proper citizenID and get the flag.
The binary features unique virtualization and is good for binary instrumentation and dynamic analysis practice.

Execution

After executing the file, a banner and prompt for input are printed. When entering a plea of entry for input, a message indicating that the ID was invalid is printed.

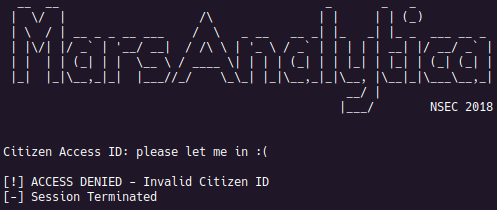
At this phase, nothing is known about the internals of the challenge. In an ideal world, we would be able to locate the negative and positive messages, assuming no obfuscation is applied to the strings. Calls to library functions to print to standard out and read from standard in may also prove to be useful, but little more can be done without reverse engineering.

File Type Identification

The file has already been identified as a 64-bit ELF file on the website that it was downloaded from. So, it was loaded into a Ghidra project and opened in the Code Browser. Upon loading, it can be seen that the entropy throughout the file is in the range [7.5, 7.7]. This challenge made no mention of a custom packer nor encryption, so this is most likely due to some well-known packing tool, like UPX. When attempting to unpack the binary using UPX, some warnings are printed, but the file is unpacked successfully and executes the same as the packed version.

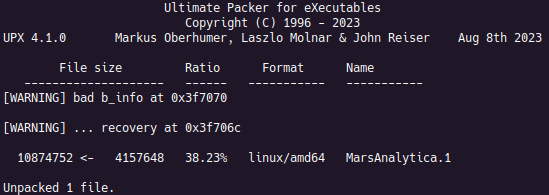
The reasoning behind the warning messages are of little importance, since they do not affect the behavior of the executable. In fact, it was unknown that there were warning messages until repeating the unpacking process after completion of the challenge to capture an image.

Static Reverse Engineering

With the challenge unpacked, it can be loaded into Ghidra and opened in the Code Browser again.

Where is the Code?

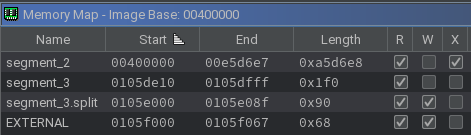
Looking at the Memory Map window, it can be seen that there are 0xA5D6E8 executable bytes, but the Functions windows shows closer to 0x800 discovered executable bytes. This indicates that there are most likely dynamic jump destinations in use. Furthermore, with virtualization, there it is not uncommon to see a segment that contains virtual code, but that is absent in this case.

The symbols of this challenge have been stripped, but the address of the _start function is still known by looking at the ELF header. This calls __libc_start_main, where the first argument (stored in RDI) is the address of main. This is nothing special, just a standard process for finding main.

Reversing Main

In an unexpected twist, main does not do much. The following steps are seen in the disassembled code:

1. Function prologue with a 0xBA4A8 byte stack frame
2. Seed randomness using a common method: srand(time(NULL)).
3. Initialize three large stack buffers.
4. Copy many bytes into a separate buffer.
5. Do six chunks of ugly math.
6. Return.

An attempt to trace the ugly math using the loaded bytes was tedious and yielded little results after the first chunk. The only bit of information that might be gathered from this is the instruction format for the virtual code, but even that is a stretch.

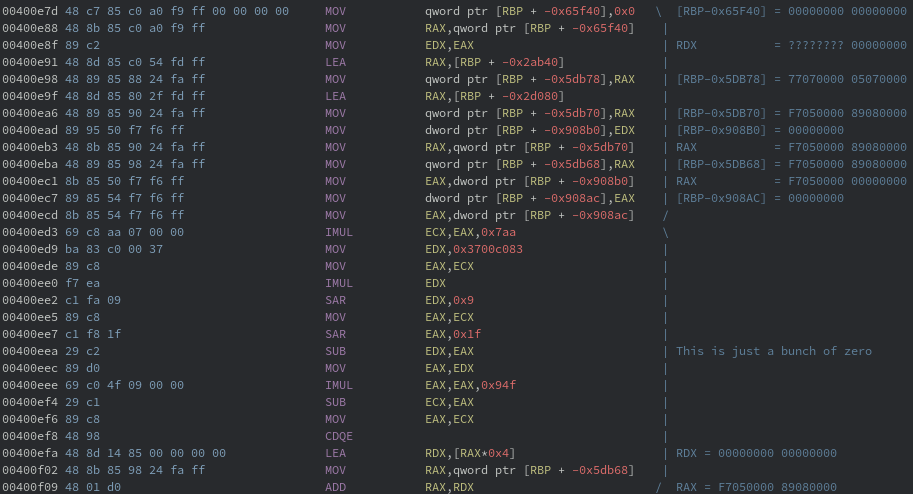
Rather than focus on repeating that process another five times, the end of the function was looked at. At the very end, an unconditional jump is made to a return statement. This is confusing, because clearly there is nothing that would print, read, nor anything else useful in main before the return.

Dynamic Reverse Engineering

Having been thoroughly confused by the static code, dynamic analysis was fallen back to. More specifically, the unpacked program was loaded using GDB so that breakpoints can be set.

First, a small complication needs to be overcome: this is a stripped executable. Breakpoints must be set using an address and the code must be stepped through at the instruction level. Ultimately, this is not a problem, but must be known before it is possible to start.

Function Discovery

After loading the challenge using GDB, a breakpoint was set at the return instruction of main (0x401149). Upon reaching the return statement, an instruction step was taken, which brought the instruction pointer to an address that was not disassembled by Ghidra (0x402335).

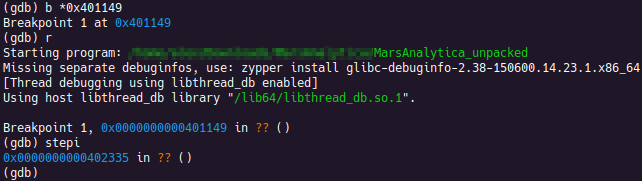
The exact way this works is not known at this time. The only way to achieve this that comes to mind is to overwrite the return address through a buffer overflow. However, there is a stack canary present, which would make that difficult to have working every time. A more thorough look at the _start and __libc_start_main function would likely yield useful information.

Nevertheless, the process of setting a breakpoint at the current function’s return and stepping into the next instruction was repeated several times. This revealed 13 functions that Ghidra did not know of, all of which performed math that would be infeasible to synthesize using only the static representation.

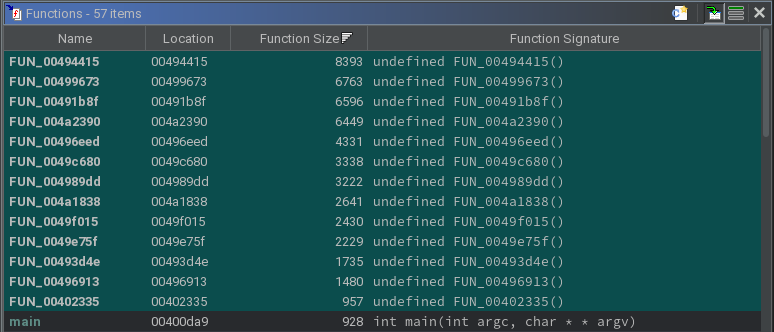
Identifying Useful Functions

To define the exact purpose of every line in every function is not a good use of time. Instead, functions that serve some important purpose were identified so that a starting point could be determined.

Looking at the Function Call Tree window for the discovered functions, there are two distinct categories of functions:

• Functions that call 0x400AAE (which calls malloc).
• Functions that call putchar, fflush, and 0x4009D7 (which calls free).

Rather than call the functions that were discovered using GDB useful, the functions that they call (but do not have a name) are decided to be useful for the following reasons: memory management is in indicator of data flow, Ghidra knew these functions existed from the beginning, and these functions are easier to understand.

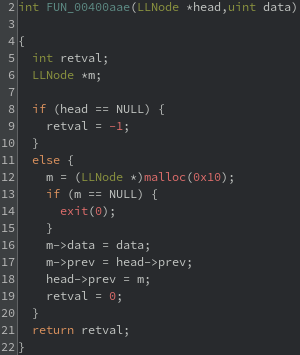
Some Malloc Function

Even without going into much detail, the decompiled code indicates that that this function is allocating some structure. Two parameters are received and stored in the allocated memory space. The first parameter is a pointer and the second parameter is some unknown, 4-byte data.

An interesting note is that the allocated memory is not returned nor freed. Instead, a status code is returned, where -1 is an error and 0 is success. Putting this all together, the assumption is that a stack node is allocated, pushed to the stack, and a pointer to the top of the stack is updated.

Some Free Function

With the knowledge of a stack node being allocated in the function that calls malloc, it is only natural to assume that the function that calls free also works with a stack node. Changing the type of the received parameter to a LLNode * and one local variable to the same type results in something that is probably as easy to read as the original source code.

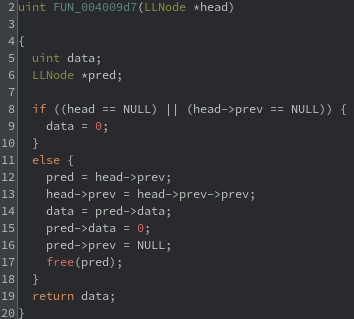
The decompiled code first validates that a null pointer exception will not occur. Then the data from the predecessor of the received parameter is saved to a local variable before clearing and freeing the predecessor. Finally, the predecessor’s data is returned.

At a higher level, this function uses the head pointer to get the data at the top of the stack and removes the node containing that data from the stack.

Choosing a Target

It can now be deduced that the math-intensive functions are in one way or another working with a user-level stack (not to be confused with the execution stack). This in and of itself is not very useful, but the data that is stored within the list may prove to be.

Based on previous work done to crack challenges made by the same author, printing of the banner is the first action that can be expected in the virtual code. Therefore, to get a better understanding of the virtual instruction set and architecture, reverse engineering of the banner will provide a known output to compare against.

Looking back at the categories of discovered functions, functions that call the 0x4009D7 function also call putchar and fflush. So, the data in the user-level stack is assumed to be the characters that make up the banner. However, to validate this, automation of dynamic analysis must take place.

Instrumentation

Similar to performing the original dynamic analysis, GDB was used to perform instrumentation.

GDB Meets Python

To get the return value of all calls to 0x4009D7 (which calls free) is trivial to automate. First, consider the manual solution:

1. Set a breakpoint at the return using GDB.
2. Run.
3. After hitting the breakpoint, print the value in RAX.
4. Continue.

Considering the banner is more than only a few characters long, repeating that process would be painful. Instead, a Python script can be developed that performs (1) and (2) at start up and repeats (3) and (4) until exiting. Furthermore, additional breakpoints and handlers can be added with ease. The Python script can be loaded using the -ex flag with GDB.

Recovering the Banner

Initially, only the aforementioned breakpoint and printing was implemented. However, the results were not as expected. Of the first 71 return values, 67 are non-printable ASCII values, while the other 5 are printable but do not appear in the banner. The characters of the banner then begin to appear, but are out of order and mixed in with character that are not in the banner.

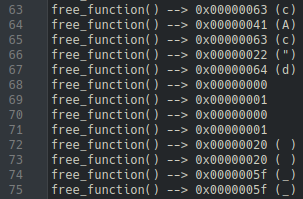
The characters were tracked in a string and printed to a file after the prompt for input by adding a breakpoint to read. The result, of course, was incomprhensible and all on one line.

An additional breakpoint was set at fflush to at least correct the single-line problem. This did not yield the banner, but a patern was noticed: at the end of every line there was a character that belonged in the banner in the correct order. All characters preceding that last character were likely for computation of the printable character. So, instead of adding a new line for fflush, the last character that was returned from the free-ing function was saved each time fflush was called. Lastly, if fflush was called twice without calling the free-ing function in between, then a new line was added for the second call to fflush. Printing the results to a file reveals the correct banner.

A Lucky Discovery

While recovering the banner included mostly pattern recognition with trial and error, a lucky discovery was made after further investigation of the return values from the free-ing function. Scrolling past the banner in the instrumentation output, the input that was provided can be seen. In other words, the input is being loaded into and read from the user-level stack.

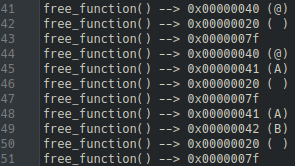
Scrolling down more introduces more usage of the input bytes, but in an unclear way. By providing different inputs and comparing the instrumentation outputs using text diff tool, it can be validated that the input is being processed in some way. Furthermore, there are values that are seen to exist on the same line regardless of what the input is (call these concrete values). With the pattern-matching brain turned on, it becomes clear that what is seen in the output is the mutation of the input bytes and comparison of that mutation to concrete values.

Satisfiability Modulo Theory (SMT)

Given that there are 21 mutation and comparison blocks, it would be nonsensical to try to come up with a value for each byte by hand. Take Image 12 as an example. The bytes at indices 1, 9, and 8 from the input (say A, B, and C) must satisfy the constraint (B * A) + C == 0x00000995. This is easy to solve by hand, but becomes more difficult as additional, overlapping constraints are added. To solve this problem, the Z3 SMT solver can be used.

Gathering Constraints

Gathering the constraints that must be satisfied was done by examining the instrumentation output. It was noted that every constraint except for the first followed the same format of

1. Input Variables
2. Intermediate Mutations
3. Concrete Value
4. Final Mutation

Where (3) and (4) are the assumed equality constraint. Recognizing this pattern made splitting the output into blocks easy. Trial and error was then used to find a mutation of (1) and (2) that results in (4).

After annotating the output with mutations that provide what is seen in (4), it was lifted into SMT-LIB. This is not a particularly pretty language, but I find it easier to work with than the Z3 API for Python or C++ since I am comfortable with lisp languages. For example, the previously mentioned constraint can be defined as follows:

(declare-const b01 (_ BitVec 32))
(declare-const b08 (_ BitVec 32))
(declare-const b09 (_ BitVec 32))
(assert (= #x00000995
           (bvadd b08
                  (bvmul b09 b01))))

Furthermore, each byte was constrained to fit in the range [0x21, 0x7E], as Image 11 appears to be enforcing.

(declare-const b00 (_ BitVec 32))
(assert (and (bvuge b00 #x00000021) (bvule b00 #x0000007E)))

Finishing Up

While implementing constraints, the tenth constraint proved to be unsatisfiable. That is, there is no combination of characters that mutate into the first ten concrete values. Rather than try to figure out where the problem lies, it was easier to reorganize my thoughts and try again from scratch, beginning with the last constraint this time. This would allow for any previously made mistakes to be a future problem.

Fortunately, after satisfying only the last constraint a change was noticed elsewhere in the instrumentation output. After all constraints but before printing the “invalid” message, there was a sequence of 21 zeroes. Now, after satisfying the last constraint, the first zero is one.

Sure enough, after satisfying the next constraint, another two zeroes flipped to one. This continued until the eleventh constraint (one before the previously unsatisfiable constraint), where all the zeroes were now one. Scrolling further into the instrumentation output, a success message was now seen to be loaded from the user-level stack.

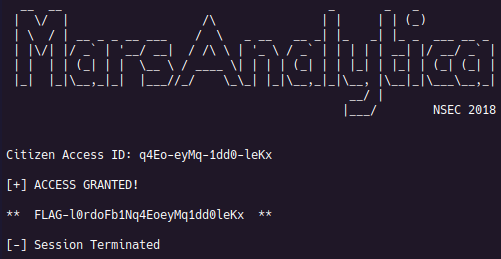
After copying the key into a non-instrumented execution, it is confirmed to be:
q4Eo-eyMq-1dd0-leKx.

Reference Code

Python Script to Instrument Using GDB

import gdb


OUTFILE = 'free_returns.txt'
bannerString = ''
lastChar = ''
printedBanner = False


"""
Print the return of a call to the freeing function
Append the return to the current run of characters
"""
def checkFreeRet():
    global lastChar

    rax = int(gdb.parse_and_eval("$rax")) & 0xFFFFFFFF

    with open(OUTFILE, 'a') as f:
        f.write(f'free_function() --> 0x{rax:08x}')
        if rax >= 0x20 and rax <= 0x7E:
            f.write(f' ({chr(rax)})')
        f.write('\n')
        try: lastChar = chr(rax)
        except: pass


"""
Update the banner string with the last character
of the current run. No run means a new line.
"""
def fflush():
    global bannerString
    global lastChar

    if len(lastChar) == 0: bannerString += '\n'
    else: bannerString += lastChar
    lastChar = ''


"""
Print the banner
Only do this once, since this "hooks" read()
"""
def printString():
    global bannerString
    global printedBanner

    if printedBanner: return
    with open(OUTFILE, 'a') as f:
        f.write(f'\n\n{bannerString}\n\n')

    printedBanner = True



# Create the output file and erase any contents
with open(OUTFILE, 'w') as f: pass

# Address that are known before execution
START       = 0x400900
FREE_FUNC   = 0x400a51
for addr in [START, FREE_FUNC]:
    bp = gdb.Breakpoint(f'*0x{addr:x}')
    bp.silent = True

# Functions that require execution to start
LIBC_READ   = 0x7ffff7d20ade
LIBC_FFLUSH = 0x7ffff7c9125e

# Start debugger
gdb.execute('run')

# Handle breakpoints based on their address
while True:
    pc = int(gdb.parse_and_eval("$pc"))

    if pc == START:
        for addr in [LIBC_READ, LIBC_FFLUSH]:
            bp = gdb.Breakpoint(f'*0x{addr:x}')
            bp.silent = True

    elif pc == FREE_FUNC: checkFreeRet()
    elif pc == LIBC_READ: printString()
    elif pc == LIBC_FFLUSH: fflush()
    gdb.execute('continue')

SMTLIB2 Constraint Definitions

;----------------------------;
; Declare the bytes of input ;
;----------------------------;
(declare-const b00 (_ BitVec 32))
(declare-const b01 (_ BitVec 32))
(declare-const b02 (_ BitVec 32))
(declare-const b03 (_ BitVec 32))
(declare-const b04 (_ BitVec 32))
(declare-const b05 (_ BitVec 32))
(declare-const b06 (_ BitVec 32))
(declare-const b07 (_ BitVec 32))
(declare-const b08 (_ BitVec 32))
(declare-const b09 (_ BitVec 32))
(declare-const b10 (_ BitVec 32))
(declare-const b11 (_ BitVec 32))
(declare-const b12 (_ BitVec 32))
(declare-const b13 (_ BitVec 32))
(declare-const b14 (_ BitVec 32))
(declare-const b15 (_ BitVec 32))
(declare-const b16 (_ BitVec 32))
(declare-const b17 (_ BitVec 32))
(declare-const b18 (_ BitVec 32))


;--------------------------------------------;
; Ensure the output is in range [0x21, 0x7E] ;
;--------------------------------------------;
(assert (and (bvuge b00 #x00000021) (bvule b00 #x0000007E)
             (bvuge b01 #x00000021) (bvule b01 #x0000007E)
             (bvuge b02 #x00000021) (bvule b02 #x0000007E)
             (bvuge b03 #x00000021) (bvule b03 #x0000007E)
             (bvuge b04 #x00000021) (bvule b04 #x0000007E)
             (bvuge b05 #x00000021) (bvule b05 #x0000007E)
             (bvuge b06 #x00000021) (bvule b06 #x0000007E)
             (bvuge b07 #x00000021) (bvule b07 #x0000007E)
             (bvuge b08 #x00000021) (bvule b08 #x0000007E)
             (bvuge b09 #x00000021) (bvule b09 #x0000007E)
             (bvuge b10 #x00000021) (bvule b10 #x0000007E)
             (bvuge b11 #x00000021) (bvule b11 #x0000007E)
             (bvuge b12 #x00000021) (bvule b12 #x0000007E)
             (bvuge b13 #x00000021) (bvule b13 #x0000007E)
             (bvuge b14 #x00000021) (bvule b14 #x0000007E)
             (bvuge b15 #x00000021) (bvule b15 #x0000007E)
             (bvuge b16 #x00000021) (bvule b16 #x0000007E)
             (bvuge b17 #x00000021) (bvule b17 #x0000007E)
             (bvuge b18 #x00000021) (bvule b18 #x0000007E)))


;------------------------------------;
; Satisfy the constraints, bottom up ;
;------------------------------------;

;--------------------------------;--------------;
; ([9] * [1]) + [8] = 0x00000995 ; 1 0x00000001 ;
;--------------------------------;--------------;
(assert (= #x00000995
           (bvadd b08
                  (bvmul b09 b01))))

;---------------------------------;--------------;
; ([7] + [12]) - [4] = 0x00000084 ; 3 0x00000001 ;
;---------------------------------;--------------;
(assert (= #x00000084
           (bvsub (bvadd b07 b12)
                  b04)))

;----------------------------------;--------------;
; ([14] ^ [6]) * [18] = 0x00002760 ; 5 0x00000001 ;
;----------------------------------;--------------;
(assert (= #x00002760
           (bvmul (bvxor b14 b06)
                  b18)))

;----------------------------------;--------------;
; ([0] + [10]) * [17] = 0x00002f76 ; 7 0x00000001 ;
;----------------------------------;--------------;
(assert (= #x00002f76
           (bvmul (bvadd b00 b10)
                  b17)))

;----------------------------------;--------------;
; ([5] + [13]) * [16] = 0x00003ac9 ; 9 0x00000001 ;
;----------------------------------;--------------;
(assert (= #x00003ac9
           (bvmul (bvadd b05 b13)
                  b16)))

;------------------------------------------;---------------;
; ([2] * [11]) + ([3] * [15]) = 0x000049c8 ; 11 0x00000001 ;
;------------------------------------------;---------------;
(assert (= #x000049c8
           (bvadd (bvmul b02 b11)
                  (bvmul b03 b15))))

;-------------------------------------------;---------------;
; ([12] - [15]) - ([4] * [18]) = 0xffffeae0 ; 13 0x00000001 ;
;-------------------------------------------;---------------;
(assert (= #xffffeae0
           (bvsub (bvsub b12 b15)
                  (bvmul b04 b18))))

;-----------------------------------------;---------------;
; ([1] * [3]) + ([6] * [11]) = 0x000045d0 ; 15 0x00000001 ;
;-----------------------------------------;---------------;
(assert (= #x000045d0
           (bvadd (bvmul b01 b03)
                  (bvmul b06 b11))))

;----------------------------------;---------------;
; ([7] ^ [14]) * [17] = 0x00001c20 ; 17 0x00000001 ;
;----------------------------------;---------------;
(assert (= #x00001c20
           (bvmul (bvxor b07 b14)
                  b17)))

;-----------------------------------------;---------------;
; ([5] - [16]) - ([0] + [2]) = 0xffffff4a ; 19 0x00000001 ;
;-----------------------------------------;---------------;
(assert (= #xffffff4a
           (bvsub (bvsub b05 b16)
                  (bvadd b00 b02))))

;------------------------------------------;---------------;
; ([8] * [10]) + ([9] + [13]) = 0x000015fe ; 21 0x00000001 ;
;------------------------------------------;---------------;
(assert (= #x000015fe
           (bvadd (bvmul b08 b10)
                  (bvadd b09 b13))))

;----------------------------------------------------------------;
; Further constraints have no impact on the number of 0x00000001 ;
; Bringing us to the final model                                 ;
;----------------------------------------------------------------;
(check-sat)
(get-model)

;-----------------------------;
; RESULT: q4Eo-eyMq-1dd0-leKx ;
;-----------------------------;

Python Script to Sort SMT Output

from z3 import *


def main():
    v = parse_smt2_file('constraints.smt2')
    solver = Solver()
    solver.add(v)

    if solver.check() == sat:
        model = solver.model()
        result = (sorted ([(v, model[v]) for v in model], key = lambda x: str(x[0])))

        s = ''
        for a in result:
            i = a[1].as_long()
            c = chr(i)
            print(f'{a[0]} = {hex(i)} ({c})')
            s += c
        print(s)

    else:
        print('unsat')


if __name__ == '__main__':
    main()