Background

CrackMe Name: Stonks
CrackMe Author: toasterbirb

CrackMe Description:
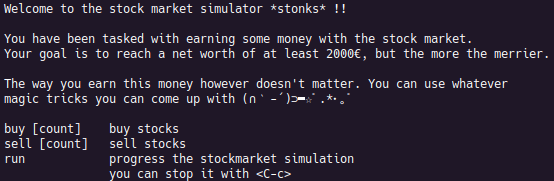
Welcome to stonks, an epic stock market simulation accessible right from the comfort of your terminal emulator. You have been tasked with achieving at least 2000€ worth of coins. You know you have reached the goal when the amount of money turns into a yellow color in the simulation screen. The way you do this is up to you.

There are multiple ways of earning the money, but here are the main goals/ideas: - Write a keygen and find valid license numbers
- Crack the binary and bypass the license check entirely
- Memory hacking
- Save file manipulation

Some of the previously mentioned methods might also require some trading skills. Everything, including patching, is allowed. Good luck with your investments!

Execution

There are four things that this challenge can perform when executed:

• Print the help message.
• Run a simple stock market simulation.
• Buy shares.
• Sell owned shares.

No matter which of those options are chosen, the “stonks” meme is saved to the working directory. Buying and selling of shares cannot be done at the same time as running the simulation, requiring the money, shares, and stock price to be saved in persistent memory.

Save File Manipulation

Since data persists through executions, it can be assumed that the PNG acts as a save file. Many file formats (PNG, MP4, ELF, and more) are defined such that appending extra data to the end of the binary will not cause problems with the behavior of the file. However, the exact file format does not need to be known. To determine where in the file the save data is being stored, the following steps were performed:

1. Run ./stonks buy 1
2. Create a copy of stonks.png.
3. Repeat until no more money is left (40 shares purchased).

Then, by converting the binary data to hexadecimal using xxd, the files can be compared using text diff tool. This leads the conclusion that the data at the end of the file does indeed relate to the save data. The way in which the bytes change has no obvious relationship to the number of money or shares owned.

To determine the format of the save file, static reverse engineering was performed in Ghidra. Starting at __libc_start_main, the main function is easily found. The decompiled code is not very pretty due to some C++ compiler garbage, but it is still very readable if the garbage is overlooked. Many functions are called, but the function at 0x103F70 is particularly interesting, since it is called before handling the specific sub-command (run, buy, or sell) and performs file manipulation. This is most likely the function responsible for loading the save data, so it will be called LoadSave.

Like main, the LoadSave function has a lot of garbage in the decompiled code. However, it is not purposefully obfuscated. As such, it is easy to pick out where the stonks.png file is being opened and read. More accurately, the first 0x89EF bytes are skipped, and the remaining 0x15C bytes are read as save data. With the data that is read from the PNG file, the following steps are performed:

1. Decrypt using an XOR cipher. The first four bytes are skipped, since they are part of the key.
2. Compute a checksum of the data. The last four bytes are skipped, since that is the checksum.
3. Compute a checksum of the stonks ELF file.
4. Write the boolean result of a checksum error at offsets 0x150 and 0x151 in the data.

An XOR cipher is fairly standard for a CTF challenge, but this exact one has been seen before. The checksum also appears to be an original algorithm. Nevertheless, they are not overly difficult, so Python can be used to decrypt the save file. After doing so, it is trivial to see that the money and shares are stored at 0x04 (int offset 0x01) and 0x08 (int offset 0x02) respectively. Everything between the shares and checksum error flags are assumed to be a history of share price.

Manipulation from here includes overwriting the values with desired numbers, correcting the data checksum (the ELF checksum is unchanged) and working backwards from decryption. This provides the first solution to the challenge, with exactly as much money as was needed to succeed: 2000€.

Click the box below to expand the Python code used to manipulate the save file.

def xor(data, key):
    res = data[:4]
    for i in range(4, len(data)):
        k = (key[(i-4) & 7] + (i-4)) % 0xff
        d = data[i]
        x = d ^ k
        res += bytes([x])
    return res


def getSaveData():
    # Read encrypted save data and its key part
    ciphertext = []
    with open('stonks.png', 'rb') as f:
        f.seek(0x89ef)
        while True:
            raw = f.read(1)
            if(not raw): break
            ciphertext.append(ord(raw))
    key = ciphertext[:4] + [0xff, 0xff, 0x07, 0x00]

    # Decrypt
    plaintext = xor(ciphertext, key)

    # Return the data and its key
    return plaintext, key


def putSaveData(plaintext, key):
    ciphertext = xor(plaintext, key)
    asBytes = b''.join([bytes([x]) for x in ciphertext])
    with open('stonks.png', 'r+b') as f:
        f.seek(0x89ef)
        f.write(asBytes)


def checksum(data):
    uVar2 = 0
    uVar1 = 1
    for i in range(len(data) - 4):
        head = data[i]
        uVar1 = (head + uVar1) % 0xFFF1
        uVar2 = (uVar1 + uVar2) % 0xFFF1
    return ((uVar2 << 16) + uVar1) & 0xFFFFFFFF


def main():
    # Decrypt the data
    plaintext, key = getSaveData()

    # Patch just enough money to reach the goal (2000 = 0x7D0)
    plaintext[4] = 0xD0
    plaintext[5] = 0x07
    plaintext[6] = 0x00
    plaintext[7] = 0x00

    # Patch a leet number of shares (1337 = 0x539)
    plaintext[8]  = 0x39
    plaintext[9]  = 0x05
    plaintext[10] = 0x00
    plaintext[11] = 0x00

    # Patch the save checksum (no need to touch the ELF checksum)
    chk = checksum(plaintext)
    plaintext[0x56 * 4 + 0] = (chk & 0x000000FF) >> 0x00
    plaintext[0x56 * 4 + 1] = (chk & 0x0000FF00) >> 0x08
    plaintext[0x56 * 4 + 2] = (chk & 0x00FF0000) >> 0x10
    plaintext[0x56 * 4 + 3] = (chk & 0xFF000000) >> 0x18

    # Encrypt the save data
    putSaveData(plaintext, key)

    # Echo the good stuff
    asInts = []
    for i in range(len(plaintext) // 4):
        d = int.from_bytes(plaintext[i*4:((i+1)*4)], byteorder='little')
        asInts.append(d)
        print(f'[{i:02x}]: 0x{d:08x}')


if __name__ == '__main__':
    main()

Binary Patching

Having learned of a checksum of the ELF file, a patching approach is the natural next solution. The idea of selling a share has not been explored, since it requires a license to be entered before the sale can succeed. However, this is the perfect use case for patching.

The location of the patch must be decided. By using Ghidra to search for the prompt to enter a key, the function to sell shares is trivially found. One benefit of patching is that it requires very little skill. Instead of trying to synthesize the function, the guard that prevents selling without a license can simply be set to a NOP sled. Now shares can be sold with or without a license, as long as there are enough shares to sell.

However, this does not solve the ELF checksum problem that was discovered during the save file manipulation solution. While it is possible to change the checksum in the file, the aim is to have the solutions be completely independent of one another. So, the value that is written as the checksum comparison is inverted. Now the checksum error flag will only be set if the checksums match (and they will not due to the patching).

While good progress, this does not technically complete the goal of reaching 2000€. For that, another patch is applied so that shares can be sold even if an insufficient amount are owned. This allows for 1 share to be purchased and 41 shares to be sold for a profit of 1000€ on a new save, thus achieving the goal. Also worth noting is how the share count did not go negative. This is because it is an unsigned integer, whose value is now: 0xFFFFFFD8.

License Generation

While patching out the need for a license is something that would successfully crack this challenge if it were seen in the “real world,” it is more interesting to create a license generator. Through the process of patching the algorithm that checks the license was found.

License validation takes place in two parts. The function at 0x103730 must return a non-zero number and the license (L) must satisfy (L * 0x283d & 0x7f) == 1.

By reverse engineering the function at 0x103730, additional constraints on the L can be determined:

• L >= 9
• L & 1 = 1
• ∀ sqrt(L) >= i >= 3, (L ≢ 0 mod i)

The last constraint may be intimidating in math notation, but is simply understood as “L is a prime number.”

A 10-line python script has been developed to generate all possible keys using the exact logic seen in the binary file. However, there are more than four billion numbers to check using a non-linear complexity algorithm, so it would take a very long time to run to completion.

import math
for L in range(3, 0xFFFFFFFF):
    i = 2
    while True:
        i += 1
        if math.floor(math.sqrt(L)) == i and (L * 0x283D) & 0x7F == 1:
            print(L)
        if L % i == 0: break

To develop a more effecient solution, C can be used for easy speed up. However, the real optimizations come in place of prime number determination. The already-covered method is the fastest way to guarantee that a number is prime, but more effecient algorithms exist to determine if a number is “probably” prime. These are usually used in cryptographic contexts, but there is no reason it cannot be applied here. The following C implementation uses the Miller-Rabin Primality Test to generate all 3,175,609 keys in 11 minutes 32 seconds. Further optimizations would use as many threads as there are CPU cores to fully utilize the computer’s processing power, but all keys have already been discovered in a reasonable amount of time.

#include <math.h>
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>


static const uint32_t PRIMES[] = { 2, 3, 5, 7 };
static const size_t PRIMES_CNT = 4;


uint32_t binpow(uint32_t base, uint32_t e, uint32_t mod) {
    uint32_t result = 1;
    base %= mod;
    while(e) {
        if(e & 1)
            result = (uint64_t)result * base % mod;
        base = (uint64_t)base * base % mod;
        e = e >> 1;
    }
    return result;
}


bool check_composite(uint32_t n, uint32_t a, uint32_t d, uint32_t s) {
    uint32_t x = binpow(a, d, n);
    if(x == 1 || x == n - 1)
        return false;

    for(uint32_t r = 1; r < s && r != 0; r++) {
        x = (uint64_t)x * x % n;
        if(x == n - 1)
            return false;
    }
    return true;
}


bool millerRabin(uint32_t n) {
    if(n < 2)
        return false;

    uint32_t s = 0;
    uint32_t d = n - 1;
    while((d & 1) == 0) {
        d = d >> 1;
        s++;
    }

    for(int i = 0; i < PRIMES_CNT; i++) {
        uint32_t a = PRIMES[i];
        if(n == a)
            return true;
        if(check_composite(n, a, d, s))
            return false;
    }
    return true;

}


int main(int argc, char *argv[]) {
    FILE *fout = fopen("keys.txt", "w");
    size_t cnt = 0;

    for(int32_t L = 3; L != 0; L++) {
        if(L % 0x100000 == 0)
            printf("Checking %u\n", L);

        if(millerRabin(L) && (L * 0x283D & 0x7F) == 1) {
            cnt += 1;
            fprintf(fout, "%u\n", L);
        }
    }

    fclose(fout);
    return 1;
}

Picking one of the random keys from the list and providing it when requested results in a successful activation, allowing for shares to be sold.

Unfortunately, the game had to actually be played to reach the 2000€ goal.